通常情况下，我们只用关注产品结构本身的强度和刚度满足一定的要求或标准即可。但实际工程中，对于像细长类的结构、薄壁结构，我们还得考虑它的稳定性问题，这也就是我们通常所说的失稳问题或者塌陷问题。

在Abaqus中，对于屈曲的计算考虑则依据结构的复杂性而定，简单的可以只考虑线性屈曲分析预估临界载荷大小；对于较复杂的模型，则可以考虑Riks 法进行后屈曲计算，从而可获取屈曲以后的结构响应情况；但对于涉及接触脱开等特别复杂的问题，可能得借助Explicit 来实现；而对于局部褶皱问题需要借助Static、Stabilize来实现。

算例—轴压薄壁圆筒的屈曲问题

E/GPa	\sigma_y/MPa	\mu	n	r/mm	L/mm
210	355	0.3	9	2000	2940

Ramberg-Osgood本构:\varepsilon=\frac{\sigma}{E}[1+\frac37(\frac{\sigma}{\sigma_y})^{n-1}]

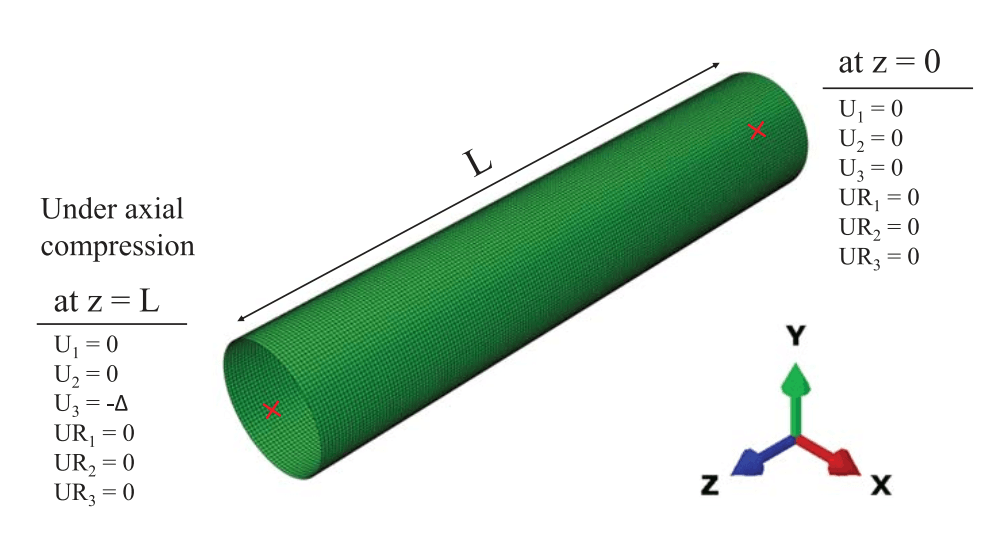
线性屈曲(特征值屈曲)

线性屈曲分析以小位移线性理论假定为基础，在结构受到荷载作用过程中忽略结构构形的变化，与结构的几何刚度矩阵有关，在一个常规的线性分析中，可以得到结构的平衡方程：

[K_E]\{u\}=\{p\}\\

其中： [K_E]为弹性刚度矩阵。如果考虑几何非线性那么平衡方程变为：

([K_E]+[K_G])\{u\}=\{p\}

在失稳情况下，假定结构的几何刚度与弹性刚度不变，可以转换为特征值问题：

del([K_E]+\lambda_G[K_{G0}])=0

式中， [K_E]——弹性刚度矩阵； [K_{G0}] ——几何刚度矩阵； \lambda_G ——特征值，即屈曲荷载与实际荷载的比值。

具体操作

调整分析步为 buck分析步，其他设置保持不变。
屈曲模态计算方法选择 子空间法。

buck modal图

buck

非线性屈曲

线性屈曲只考虑了材料在弹性阶段的行为，且在载荷作用过程中忽略了结构构型的变化，假定结构构型不发生变化；然而在实际的结构中存在材料非线性、结构非线性与几何缺陷的影响，这显然是过于保守的分析，其极限荷载较线性屈曲荷载明显降低。因此为了得到更接近实际的失稳荷载，应对结构进行考虑结构非线性、材料非线性以及初始几何缺陷影响的非线性屈曲分析。在有限元分析中，弧长法（Arc Length Method）是一种用于解决非线性结构问题的数值计算方法，它主要用于处理非线性材料行为、大变形、接触、摩擦等引起的问题，这些问题通常无法简单地使用线性方法进行分析。在结构非线性屈曲分析过程中的平衡方程为:

F(u,\lambda)=q_{int}(u,\lambda)-\lambda q_{ext}=0\\ \lambda_{i+1}=\lambda_i+\Delta \lambda_{i+1}\\ u_{i+1}=u_i+\Delta u_{i+1}

式中 F(u,\lambda)——不平衡矢量；q_{ext} ——施加的外力矢量； q_{int} ——内力矢量； \Delta u_i——第i个增量步的总位移； \Delta\lambda_i——第i个增量步的总荷载增量。

在弧长法计算的过程中，根据平衡路径的不同，结构的非线性屈曲分为两种，分叉屈曲与曲极值屈曲，两种屈曲的表现形式如图3所示，P_{ca}是临界载荷值。

这里使用弧长法进行非线性屈曲分析，调整分析步为 risk分析步，其他设置保持不变。

注意:

risk需要设置最终止标准，最大位移或者最大载荷比例因子，不然分析不会停止，需要手动终止。

最大增量步需要调整100步不够，初始增量步不能太大。

几何结构的真实缺陷形状往往是不易得到的，下面介绍几种在数值仿真中常见的几何缺陷。

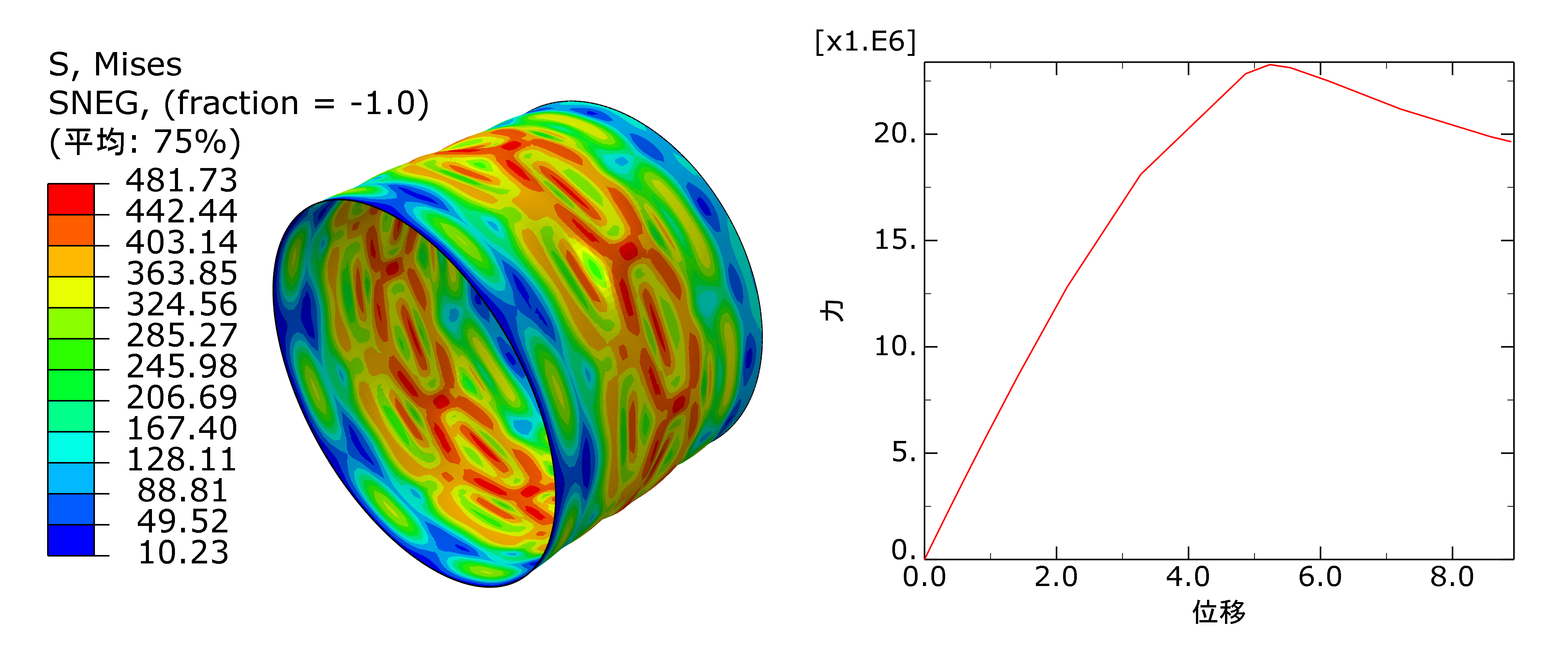
线性特征值屈曲模态缺陷

施加方法：取圆柱壳线性特征值屈曲模态变形作为结构的初始几何缺陷形貌，再乘以一个缺陷幅值系数。具体步骤如下。

在buck分析的 buck.inp文件中添加下面两行关键字,可以得到线性屈曲分析的位移结果文件—buck.fil。
```
*node file
u
##在*output,history后面添加
```
在risk分析的 risk.inp文件中添加如下关键字
```
*IMPERFECTION,FILE=buck, step=1
1,13
```
在*Step前面添加，buck为buck.fil的文件名，step=1表示第1个分析步，1表示第一阶模态，13为缺陷系数。缺陷幅值等于缺陷系数乘以1。

Dimple-Like 缺陷

表达式

w=-w_0e^{-(x/L_1)^2}e^{-(\theta/\theta_1)^2}

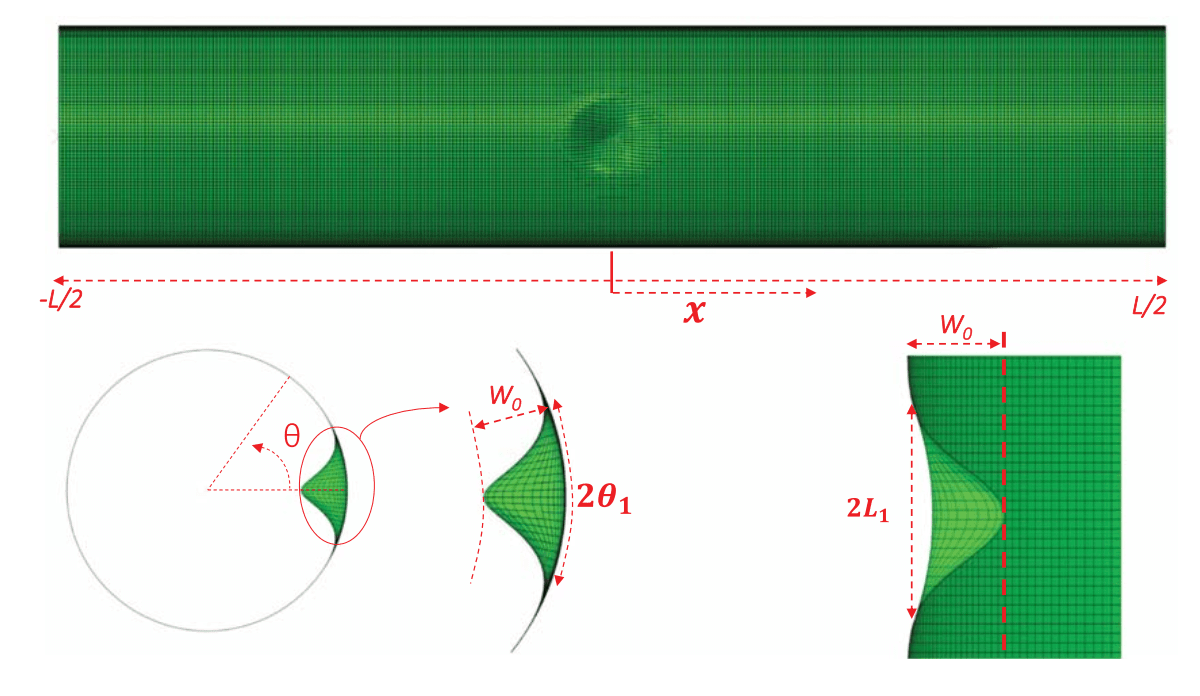
这里使用改变节点坐标的方式，添加缺陷，使用 python修改 inp文件。

import numpy as np
with open('C:/Users/xy/Desktop/nice/circular.inp','r') as f:##inp文件原始路径
    lines = f.readlines()
    for i in range(len(lines)):
        if '*Node' in lines[i] and i<20:
            start=i+1
        if "*Element" in lines[i] :
            end=i
L1,w0=100,13
theta1=np.pi/36 
for i in range(start,end):
    number= int(lines[i].split(',')[0])
    point_x = float(lines[i].split(',')[1])
    point_y = float(lines[i].split(',')[2])
    point_z=float(lines[i].split(',')[3])
    if point_x>0:
        x=point_z - 2940 / 2
        theta=np.arcsin(point_y / np.sqrt(point_x ** 2 + point_y ** 2))
        w=-w0*np.exp(-(x/L1)**2)*np.exp(-(theta/theta1)**2)
        r=np.sqrt(point_x ** 2 + point_y ** 2)+w
        point_x,point_y=r*np.cos(theta),r*np.sin(theta)
        lines[i]=f"{number},{point_x},{point_y},{point_z} \n "
with open('C:/Users/xy/Desktop/nice/circular-c.inp', 'w') as f:##修改后的inp文件
     f.writelines(lines)

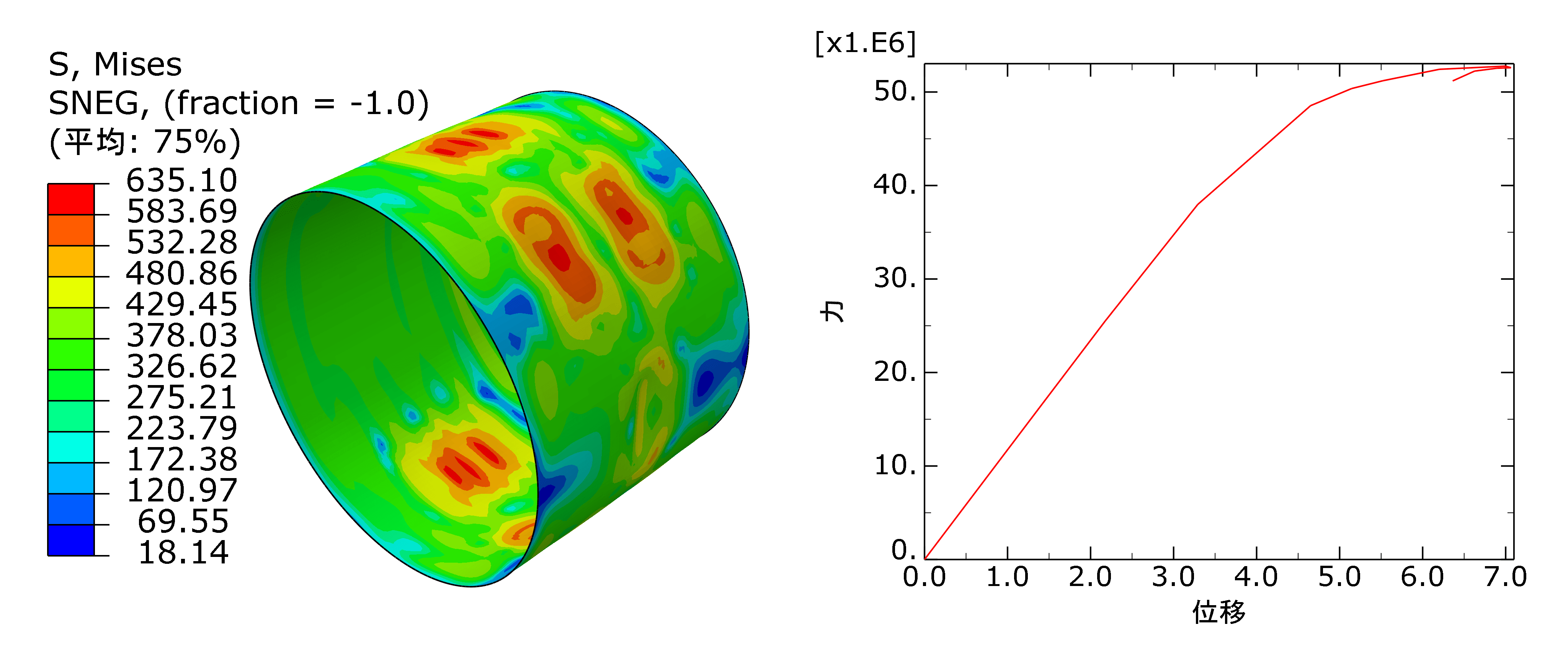
risk-smises2