轴套过盈配合优化设计
研究对象
轴套与轴,椭圆轴的长半轴 b=30mm,短半轴a=20mm,在abaqus中建立二维四分之一模型,设置模型的法向过盈量为0.1mm,轴套在椭圆轴短半轴方向厚度为2.0mm,弹性模量参数如下,轴为210Gpa,轴套为100Gpa。
在这里,轴套的内轮廓为椭圆曲线已经确定,我们只需对模型的外轮廓参数化,按角度均分轴套的内轮廓,延长各段的内轮廓法线,连接各段的法线终点可以得到轴套,这里只需要控制各段法线长度d不同,就可以控制轴套截面厚度变化。理论上来说均分的数量越多,模型描述越精确,为了计算的效率考虑,将内轮廓均分为20分,模型输入参数为(d0,d1,d2,……),得到如下图的参数化模型。


设计要求
在配合完成后,沿轴套内表面各处的最大主应力均匀分布,即最大主应力一致。
有限元分析中的问题
由于使用了四分之一模型, 边界条件为X轴与Y轴对称约束,单元类型为平面应变四边形单元(CPE4)。
在abaqus中,过盈配合的实现方式有两种方式,一种是在相互作用里面给定过盈配合的值,一种是在几何上制造过盈配合,本模型采用第二种方式实现过盈配合。
优化过程
在前面的参数化建模中,已经实现了轴套的参数化,轴套的外轮廓可以用一个厚度的序列来表述。对模型优化的过程就是,求解最优化序列的过程,设计目标为找到某一种轮廓线使得轴套内轮廓上最大主应力的极差值最小。
如果直接对每个位置处的厚度取值限定一个范围,然后使用搜索算法对每种组合方式进行有限元分析那么可能结果有多种方式,找到最优解是一个不现实的算法。这里需要抓住这个问题的特点来进行分析,可以从圆轴与圆形轴套配合的情况得到启发,从经典弹性力学中可以获得在过盈配合中轴套内表面的最大主应力为:
对不同的轴套厚度t,可以计算出轴套内表面环向应力的数值,如下图所示,应力随轴套厚度增大而减小。借鉴上面的圆形轴套得出的结论,假定认为对于椭圆形轴套也存在相同的结论,当增大轴套第i号位置处的厚度后,同样会减小轴套内表面第i号位置处的应力,轴套其他位置的厚度对i号位置内表面的应力影响较小。

现在可以设计这样一个算法,将系统的输入(轴套不同位置处的厚度值)记作:
而将系统的输出(轴套内轮廓不同位置处的第一主应力值)记作:
存在函数关系:
从上面的分析可以得到下面两个条件:
考虑到牛顿迭代法求解非线性方程的过程,利用泰勒展开公式将y_i在处x_i一次展开。x_i对y_i的贡献远大于其他位置的厚度,所以只保留y_i对x_i分量的微分:
构建出如下迭代公式:
其中,y_{1r}为前次迭代的应力参考值,x_{1i}为前次迭代轴套第i号位置处的截面厚度,x_{2r}为当前迭代中轴套第i号位置处的截面厚度。若当前轴套某处应力值偏大,则使用应力相对差异值修正该处的厚度,进而该处应力减小,使得系统的应力分布情况向均匀分布方向发展。
计算结果
等厚度轴套计算结果
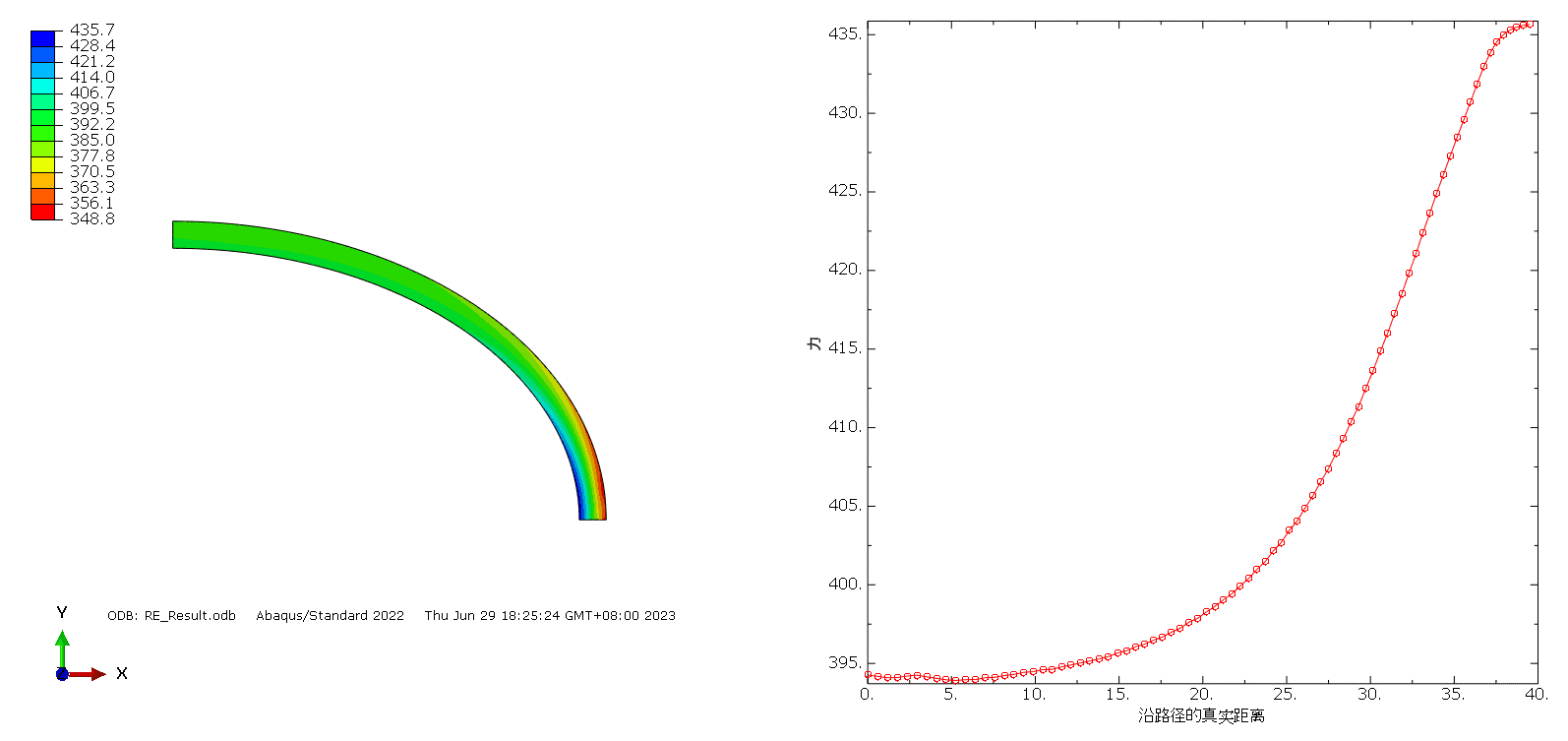
优化计算结果
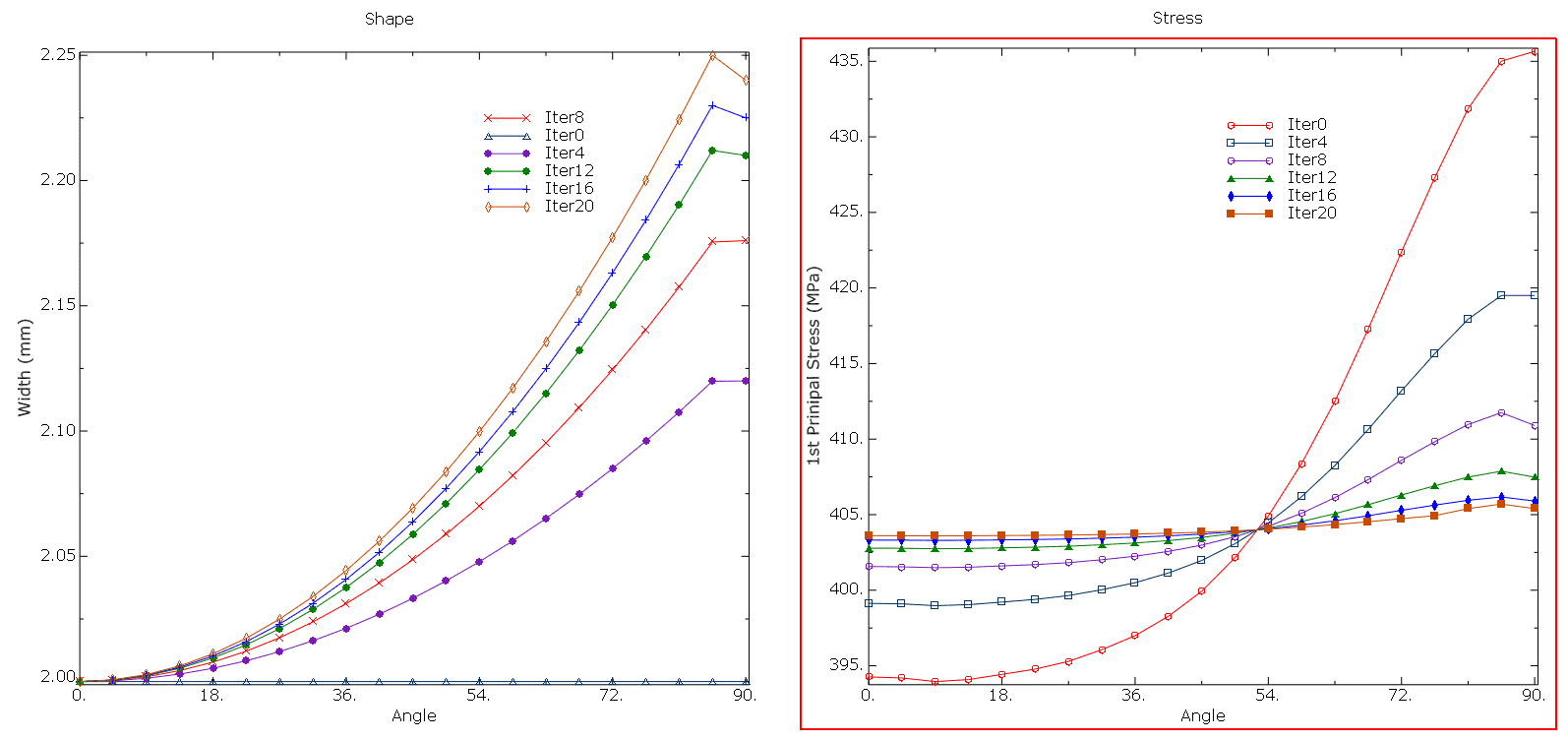
轴套内轮廓最大主应力逐渐趋向一致,最终经过20次迭代,第一主应力最大值与最小值的差距从开始的41.7Mpa减小到1.5Mpa


